 Bueno, en realidad no es cosa solo de JavaScript sino que esto ocurre en la mayor parte de los lenguajes de programación, incluyendo C# o Java, pero me centraré en JavaScript porque es el que más utilizo y en el que más fácil lo puedes probar (tan solo abre tu navegador y pulsa F12).
Bueno, en realidad no es cosa solo de JavaScript sino que esto ocurre en la mayor parte de los lenguajes de programación, incluyendo C# o Java, pero me centraré en JavaScript porque es el que más utilizo y en el que más fácil lo puedes probar (tan solo abre tu navegador y pulsa F12).
Lo que voy a contar no es más que una curiosidad en la mayor parte de los casos, con poca incidencia práctica, pero creo que puede resultar muy interesante para algunos de los lectores de este blog.
En matemáticas existe el concepto de límite, que se refiere a la aproximación de una fórmula o proceso hacia un valor concreto. Por ejemplo, si consideramos la sucesión de divisiones que dan como resultado dividir el número 1 entre todos los números naturales (del 1 a infinito, uno detrás de otro, vamos), así:
1/1, 1/2, 1/3, 1/4.... hasta 1/∞
el resultado de cada división es cada vez más pequeño (1, 0.5, 0.333333, 0.25...) y llega un momento, con números grandes, en el que la diferencia entre una división y la siguiente es tan pequeña que solo se ve en decimales muy altos. Es decir, cuando el número que tenemos debajo aumenta mucho, el resultado práctico es un cero. Por eso se dice que esta serie converge al límite 0.
Ya está bien de matemáticas. Lo que quería explicar es que esta sucesión de divisiones se acerca cada vez más al número 0, pero como existen infinitos números, en realidad nunca llega a cero del todo, sino que tiende a ser 0, pero no lo es. ¿Y entonces qué es? Pues algo muy parecido al 0 pero un poquito (casi nada) mayor que cero.
Si abres la consola de tu navegador y divides 1 entre un montón de nueves (para hacer un número grande) obtienes algo similar a esto:
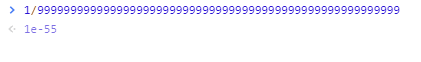
Esto significa que el resultado de esa división es un 0 seguido de 54 ceros decimales y luego un 1. Algo que no es cero, pero poca diferencia tiene con él.
Si lo llevamos al límite y dividimos por infinito (en JavaScript -Infinity o bien la propiedad POSITIVE_INFINITY de la clase Number), obtenemos:
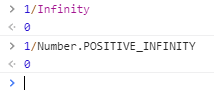
Efectivamente: 0. Pero este cero es un "cero positivo" ya que el resultado de la división se acerca todo lo posible a 0 por el lado positivo.
Esto te puede parecer una tontería porque al fin y al cabo se ve igual que un cero, pero si ahora hacemos lo mismo con números negativos (en el numerador o en el denominador), la cosa cambia un poco:

En efecto, ahora sí, verás por pantalla un ¡cero negativo!. Míralo más de cerca:

En este caso sí muestra el signo por ser negativo (los números positivos no se muestran con el + delante, porque va implícito), evidenciando lo que explicaba antes de que el resultado de la división es el límite de una serie convergente.
No hace falta tener una serie convergente para obtenerlos. Los podemos declarar directamente de la siguiente manera:
var ceroPos = +0;
var ceroNeg = -0;
y tendremos los mismos valores que obtendríamos de hacer las divisiones anteriores.
Vale. Pues bien. Ahora ya sabes que tenemos dos ceros diferentes en el lenguaje. ¿Qué pasa con ellos?
¿Qué pasa si hacemos una comparación?
Por ejemplo, ¿cuál será el resultado de comprar las dos variables anteriores?:

De entrada podría parecer que no son iguales, ya que uno es algo que tiende a cero por la derecha y el otro por la izquierda (positivo y negativo), pero el resultado es true, o sea, JavaScript los considera iguales. De hecho los comparadores < o > darían siempre false precisamente porque los considera iguales aunque no lo sean.
Pero, si son iguales ¿porqué los representa de manera diferente?
Esto tiene que ver con la manera de representar los números que tienen la mayor parte de los lenguajes de programación: el estándar IEEE 754. Para resumir de manera rápida y aproximada, en este estándar de representación, los números que pueden ser positivos y negativos se representan en binario reservando un bit para el signo. Este bit de signo se establece siempre, independientemente de la magnitud que estemos representando. En el caso extremo del 0 también, por eso el cero negativo no es más que un cero con el bit de signo establecido.
De hecho, como el 0 positivo no es más que un cero con el bit de signo sin establecer, el cero "total" (es decir, no resultado de una serie convergente como hemos visto, sino simplemente establecido como var cero = 0; por ejemplo) es en realidad un cero positivo o +0. No hay diferencia.
¿Qué pasa si hacemos operaciones matemáticas con ellos?
Pues depende. En el caso de sumas y restas, no es posible obtener un -0 salvo si el único operando es un -0 (por ejemplo, sumando o restando -0 consigo mismo). En el resto de operaciones (por ejemplo multiplicaciones, divisiones o restos/módulos), se siguen las reglas normales de operar con signos (negativo por positivo = negativo, ya sabes):

Conversión a y desde cadenas de texto
Para las pruebas que has visto he utilizado la consola del navegador, que muestra directamente los valores "reales" de los resultados y variables. Pero si tú haces la prueba utilizando un archivo .js y mostrando cosas con alert(), no verás el -0 por ningún lado. Por ejemplo:
alert(ceroNeg);
mostraría simplemente un 0 por pantalla.
El motivo de esto es que el método toString() por defecto, el que está definido en la clase base de todas (Object), convierte el número 0 negativo en un simple 0, y alert() llama a toString() por debajo antes de mostrar algo por pantalla. Lo mismo ocurriría si hacemos concatenaciones de valores forzando la conversión a texto, como por ejemplo:

Como ves, al forzar la conversión a cadena del -0 se queda simplemente en 0, por lo que no verás un "5-0" como resultado que sería lo que podríamos esperar. Hay que saberlo.
Otro efecto que tiene esto es que, si para nuestra aplicación es importante tener esta diferencia entre ceros controlada (por ejemplo, si es un algoritmo matemático que lo necesita) y debemos enviar datos al servidor, tenemos que saber que al convertir con stringify() la información numérica a JSON para enviarla al servidor, se va a perder este signo negativo:

Fíjate en como, al pasarlo a cadena JSON, el signo se pierde. Es algo que en casos muy concretos puede ser un problema, y hay que tenerlo en cuenta.
Y qué pasa si queremos utilizar parseInt() o parseFloat() para realizar la operación inversa, es decir, obtener un número desde una cadena de texto. Veamoslo:

Como se puede observar, las operaciones de "parseo" (interpretación y conversión) de una cadena a número sí tienen en cuenta esa diferencia y generan el valor correcto.
¿Cómo distingo entre un cero negativo y uno positivo si tengo necesidad?
Como hemos visto antes, si comparamos dos ceros del signo que sean, JavaScript los considera iguales. Entonces ¿cómo logro distinguir uno del otro?
Una primera idea podría ser usar el signo con Math.sign() que devuelve 1 para los números positivos y -1 para los negativos. Pero, oh sorpresa, con el -0 se comporta de otro modo:
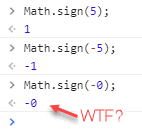
Devuelve un -0, por lo que estamos como al principio y no podríamos usarlo para la comparación (no puedes comprobar la igualdad de -0 porque siempre será positiva para 0 y para -0).
Entonces ¿qué hacemos?
Bien, No podemos comparar directamente el 0 y el -0, pero sí podemos compararlos indirectamente si usamos resultados de utilizarlos. Por ejemplo en una multiplicación o una división que, como hemos visto, conservan el signo correctamente. Por lo tanto, si dividimos un número entre -0 debería darnos -Infinity, cosa que no ocurrirá con ningún otro número. Así que nuestra función podría ser:
function esCeroNegativo(n) {
//Primero comprobamos que es un número lo que se nos pasa
if (isNaN(n)){
throw new RangeError('¡Debes facilitar un número!')
}
//compramos la división con -infinito
return (1/n == -Infinity);
}
De este modo podremos saber si el número que le estamos pasando es o no un -0:

En resumen
En este artículo hemos estudiado que en JavaScript, al igual que en muchos otros lenguajes, existen en realidad dos ceros y no solo "el cero", al que estamos acostumbrados. Aunque es algo que en la mayor parte de los casos se queda tan solo en una curiosidad sin impacto en la práctica, es un tema interesante per se, para conocer cómo funciona nuestro lenguaje favorito por debajo del capó, pero que en ciertas aplicaciones muy especializadas podría ser importante. Y es que en programación las ocasiones especiales son las que lo joroban todo muchas veces, y conocer este tipo de frikadas es lo que marca la diferencia 😉
Espero que en cualquier caso te haya parecido interesante.
💪🏻 ¿Este post te ha ayudado?, ¿has aprendido algo nuevo?
Pues NO te pido que me invites a un café... Te pido algo más fácil y mucho mejor
